Principal Component Analysis (PCA) in R
- Martin Calvino

- Nov 15, 2021
- 18 min read
Updated: Nov 20, 2021
Computational approaches designed to address the inter-relationship present among the variables in a dataset are essential techniques when trying to understand the complexity of information. Principal components and exploratory factor analysis are two methodologies used to explore and simplify multivariate data.
In principal component analysis (herein PCA), a great number of correlated (and perhaps redundant) variables are transformed into a smaller set of uncorrelated variables known as principal components (here in PCs). Principal components are thus uncorrelated composite variables that retain the most information from the original variables in the dataset.
Exploratory factor analysis (EFA) on the other hand, uncover the latent structure present in the variables of a dataset. This means that the complexity of information can be explained by a smaller set of latent constructs explaining the relationship among variables in the dataset.
Here I will focus on how to implement PCA in R, and will explain EFA in a separate text.
The base installation of R provide us with functions to perform PCA: mainly princomp() and prcomp() respectively. While princomp() implements Spectral Decomposition (evaluates correlations among variables), prcomp() and the PCA() function (from the FactoMineR package) use Singular Value Decomposition (evaluates the correlations among individuals). In this work I will be using prcomp().
The most common steps in PCA are:
1 Prepare data -
Input is either a raw data matrix or a correlation matrix. Remove missing values from dataset before proceeding. Inspect dataset for outliers and remove them. You may also consider trimming the extreme values at each end of your dataset. If variables in dataset have quite different range of values, then scale (and center) variables prior to performing PCA.
2 Decide how many components to extract -
There are several criteria to decide on the number of principal components to extract: (a) decide on number of components based on previous experience and domain knowledge; (b) decide on number of components based on a minimum percentage of cumulative variance in the variables from the dataset (for instance, you may want to retain all components that together account for 75% of cumulative variance); (c) decide on the number of components to extract based on eigenvalues.
3 Extract components -
Extract the principal components (PCs).
4 Rotate components -
Rotations are a group of mathematical approaches for transforming the component loadings matrix into one's that is more interpretable. Rotation methods could result in uncorrelated components (orthogonal rotation) or allowed to correlate (oblique rotation). Rotation is performed when the PCs are difficult to interpret.
5 Interpret results -
Interpret the proportion of variance explained by the principal component for each variable.
6 Compute components scores -
The goal is to replace a larger set of correlated variables with a smaller set of derived variables.
In this work I perform all the above stepts except rotating components and computing components scores.
Prepare data -
The data I focus on contains mortgage applications in the state of New Jersey for the years 2018, 2019 and 2020 respectively. These datasets were previously filtered based on two ethnic groups: (1) not.hispanic; and (2) latino applicants, respectively. I obtained them from the Consumer Financial Protection Bureau's website and they are associated with the Home Mortgage Disclosure Act (HMDA) that requires financial institutions to disclose loan-level information about mortgages. I've previously performed hierarchical clustering analysis on the dataset corresponding to the year 2018.
#mortgage applications for the year 2018 as 'may18'
may18 <- read.csv(file.choose()) #load dataset
str(may18) #data frame containing 295,286 observations and 99 variables
#mortgage applications for the year 2019 as 'may19'
may19 <- read.csv(file.choose()) #load dataset
str(may19) #335,661 observations and 99 variables
#mortgage applications for the year 2020 as 'may20'
may20 <- read.csv(file.choose()) #load dataset
str(may20) #486,304 observations and 99 variables
#merge datasets
comb.data18_19 <- merge(may18, may19, all=TRUE)
comb.data18_19_20 <- merge(comb.data18_19, may20, all=TRUE)
str(comb.data18_19_20) #1,117,251 observations & 99 variables
We can observe that when combined, we have information from 1,117,251 loan applicants from 2018 to 2020. During these tree years, a total of 1,061 lending institutions (banks and credit unions) received loan applications all across the state of New Jersey.
#how many banks received applications?
banks <- factor(comb.data18_19_20$lei)
length(levels(banks)) #1,061 lending institutions (banks)
The number of loan applications increased year to year, from 295,286 in 2018 to 486,304 in 2020 (Figure 1). However, the proportion of latino applicants remained similar, from 11.84% for 2018 to 12.21% for 2019 and 11.06% for 2020 (Figure 1). It is interesting to note that while the number of applications increased by 1.45 times from 2019 to 2020; loan applications from the latino community dropped 1.15% for the same period, when the pandemic had it heist in New Jersey and the country.
#plot data
library(ggplot2)
ggplot(data=comb.data18_19_20) + geom_bar(mapping = aes(x=activity_year, fill=derived_ethnicity)) + labs(title="Loan Applicants Per Year")
ggplot(data=comb.data18_19_20, aes(x=activity_year, fill=derived_ethnicity)) + geom_bar(position='fill') + labs(title="Proportion of Loan Applicants Per Year")
Figure 1. Loan applicants per year (left: count and right: proportion) for the state of New Jersey were visualized according to the ethnicity (latino vs not.hispanic) of the applicant.
Next, I selected variables of interest from the 99 variables available in each dataset and thus reduced the complexity of the information. Within the selected variables, I will later run PCA only on numeric (continuous) variables.
#select variables of interest
#not.hispanic18.bank as nh18b
nh18b <- not.hispanic18$lei
#not.hispanic18.race as nh18r
nh18r <- not.hispanic18$derived_race
#not.hispanic18.sex as nh18s
nh18s <- not.hispanic18$derived_sex
#not.hispanic18.action_taken as nh18at
nh18at <- not.hispanic18$action_taken
#not.hispanic18.loan_amount as nh18la
nh18la <- not.hispanic18$loan_amount
#not.hispanic18.property_value as nh18pv
nh18pv <- as.numeric(not.hispanic18$property_value)
#not.hispanic18.income as nh18i
nh18i <- as.numeric(not.hispanic18$income)*1000
#not.hispanic18.tract_median_age_of_housing_units as nh18mah
nh18mah <- not.hispanic18$tract_median_age_of_housing_units
#not.hispanic18.selectedVariables as 'nh.18.sV'
nh.18.sV <- data.frame(nh18b, nh18r, nh18s, nh18at, nh18la, nh18pv, nh18i, nh18mah)
str(nh.18.sV)
#not.hispanic19.bank as nh19b
nh19b <- not.hispanic19$lei
#not.hispanic19.race as nh19r
nh19r <- not.hispanic19$derived_race
#not.hispanic19.sex as nh19s
nh19s <- not.hispanic19$derived_sex
#not.hispanic19.action_taken as nh19at
nh19at <- not.hispanic19$action_taken
#not.hispanic19.loan_amount as nh19la
nh19la <- not.hispanic19$loan_amount
#not.hispanic19.property_value as nh19pv
nh19pv <- as.numeric(not.hispanic19$property_value)
#not.hispanic19.income as nh19i
nh19i <- as.numeric(not.hispanic19$income)*1000
#not.hispanic19.tract_median_age_of_housing_units as nh19mah
nh19mah <- not.hispanic19$tract_median_age_of_housing_units
#not.hispanic19.selectedVariables as 'nh.19.sV'
nh.19.sV <- data.frame(nh19b, nh19r, nh19s, nh19at, nh19la, nh19pv, nh19i, nh19mah)
str(nh.19.sV)
#not.hispanic20.bank as nh20b
nh20b <- not.hispanic20$lei
#not.hispanic20.race as nh20r
nh20r <- not.hispanic20$derived_race
#not.hispanic20.sex as nh20s
nh20s <- not.hispanic20$derived_sex
#not.hispanic20.action_taken as nh20at
nh20at <- not.hispanic20$action_taken
#not.hispanic20.loan_amount as nh20la
nh20la <- not.hispanic20$loan_amount
#not.hispanic20.property_value as nh20pv
nh20pv <- as.numeric(not.hispanic20$property_value)
#not.hispanic20.income as nh20i
nh20i <- as.numeric(not.hispanic20$income)*1000
#not.hispanic20.tract_median_age_of_housing_units as nh20mah
nh20mah <- not.hispanic20$tract_median_age_of_housing_units
#not.hispanic20.selectedVariables as 'nh.20.sV'
nh.20.sV <- data.frame(nh20b, nh20r, nh20s, nh20at, nh20la, nh20pv, nh20i, nh20mah)
str(nh.20.sV)
#latino18.bank as la18b
la18b <- latino18$lei
#latino18.race as la18r
la18r <- latino18$derived_race
#latino18.sex as la18s
la18s <- latino18$derived_sex
#latino18.action_taken as la18at
la18at <- latino18$action_taken
#latino18.loan_amount as la18la
la18la <- latino18$loan_amount
#latino18.property_value as la18pv
la18pv <- as.numeric(latino18$property_value)
#latino18.income as la18i
la18i <- as.numeric(latino18$income)*1000
#latino18.tract_median_age_of_housing_units as la18mah
la18mah <- latino18$tract_median_age_of_housing_units
#la18.selectedVariables as 'la.18.sV'
la.18.sV <- data.frame(la18b, la18r, la18s, la18at, la18la, la18pv, la18i, la18mah)
str(la.18.sV)
#latino19.bank as la19b
la19b <- latino19$lei
#latino19.race as la19r
la19r <- latino19$derived_race
#latino19.sex as la19s
la19s <- latino19$derived_sex
#latino19.action_taken as la19at
la19at <- latino19$action_taken
#latino19.loan_amount as la19la
la19la <- latino19$loan_amount
#latino19.property_value as la19pv
la19pv <- as.numeric(latino19$property_value)
#latino19.income as la19i
la19i <- as.numeric(latino19$income)*1000
#latino19.tract_median_age_of_housing_units as la19mah
la19mah <- latino19$tract_median_age_of_housing_units
#latino19.selectedVariables as 'la.19.sV'
la.19.sV <- data.frame(la19b, la19r, la19s, la19at, la19la, la19pv, la19i, la19mah)
str(la.19.sV)
#latino20.bank as la209b
la20b <- latino20$lei
#latino20.race as la20r
la20r <- latino20$derived_race
#latino20.sex as la20s
la20s <- latino20$derived_sex
#latino20.action_taken as la20at
la20at <- latino20$action_taken
#latino20.loan_amount as la20la
la20la <- latino20$loan_amount
#latino20.property_value as la20pv
la20pv <- as.numeric(latino20$property_value)
#latino20.income as la20i
la20i <- as.numeric(latino20$income)*1000
#latino20.tract_median_age_of_housing_units as la20mah
la20mah <- latino20$tract_median_age_of_housing_units
#latino20.selectedVariables as 'la.20.sV'
la.20.sV <- data.frame(la20b, la20r, la20s, la20at, la20la, la20pv, la20i, la20mah)
str(la.20.sV)
Now let's inspect these dataset for any missing values using the VIM library (Figure 2). This approach identified the variable property_value (pv) as the one having more occurrences of missing values in all datasets (Figure 2). Income was also a variable harboring missing values in all datasets. Race was a variable with missing values for the year 2018. It is interesting to note that for the years 2018 and 2020, there were many observations in which missing values for the variable property_value co-occurred with missing values for the variable income.
#visualize and remove missing values (NAs)
library(VIM)
#the aggr() function depicts the missing values (in counts or percentage) for each variable alone or in combination with each other
aggr(nh.18.sV, prop=FALSE, numbers=TRUE)
#the matrixplot() function depicts missing data (in red) for each observation in the data frame
#values for each variable are rescaled to the interval [0,1] and represented by grey colors (lighter colors > lower values / darker colors > higher values)
matrixplot(nh.18.sV)
aggr(nh.19.sV, prop=FALSE, numbers=TRUE)
matrixplot(nh.19.sV)
aggr(nh.20.sV, prop=FALSE, numbers=TRUE)
matrixplot(nh.20.sV)
aggr(la.18.sV, prop=FALSE, numbers=TRUE)
matrixplot(la.18.sV)
aggr(la.19.sV, prop=FALSE, numbers=TRUE)
matrixplot(la.19.sV)
aggr(la.20.sV, prop=FALSE, numbers=TRUE)
matrixplot(la.20.sV)
Figure 2. Visualization of missing values for each group of datasets assembled based on ethnicity (not.hispanic vs latino) . Top 6 panels: output of the aggr( ) function from the VIM package visualizing missing values (shown in red) for each variable in the dataset (left sub-panel), and for the combination of variables (right sub-panel). Bottom 6 panels: output of the
matrixplot( ) function from the VIM package visualizing missing values for each (and all) observations / loan applications in the dataset. Missing values are shown in red, whereas all other values are scaled between 0 to 1 and colored in gray scale: lower values are lighter whereas higher values are darker.
Let's now remove all missing values.
#remove missing values
nh.18.sV <- na.omit(nh.18.sV) #193,669 observations & 8 variables
nh.19.sV <- na.omit(nh.19.sV) #218,848 observations & 8 variables
nh.20.sV <- na.omit(nh.20.sV) #313,849 observations & 8 variables
la.18.sV <- na.omit(la.18.sV) #22,695 observations & 8 variables
la.19.sV <- na.omit(la.19.sV) #29,198 observations & 8 variables
la.20.sV <- na.omit(la.20.sV) #35,270 observations & 8 variables
We now inspect the datasets to have a better sense of their statistics using the describe( ) function from the psych package.
#inspect the statistics of each dataset using the describe() function from the psych package
library(psych)
#columns 5 to 8 are numberic values in each dataset
describe(nh.18.sV[, c(5:8)])
describe(la.18.sV[, c(5:8)])
describe(nh.19.sV[, c(5:8)])
describe(la.19.sV[, c(5:8)])
describe(nh.20.sV[, c(5:8)])
describe(la.20.sV[, c(5:8)])

We can observe that the variable income (i) for both not.hispanic and latino applicants displays negative values and its range is the biggest among the four variables; while the range for the variable median_age_of_house (may) is the smallest. This means the variables need to be scaled prior to implementing PCA. We also see that the maximum values for the first 3 variables are quite distant from the median, meaning that outliers should be identified and removed prior to implementing PCA.
One of the approaches used to identify outliers in a dataset is the Interquartile Range (IQR) method; which takes the central 50% area located between the 75th and 25th percentile of a distribution. If a data point is located above the 75th percentile by a factor of 1.5 times the IQR, it is considered an outlier. Similarly, a data point is an outlier if it is located below the 25th percentile by a factor of 1.5 times the IQR. We can visualize outliers using boxplots in the following manner:
boxplot(dataset)$out Results are shown on Figure 3.
#visualize outliers using boxplot(dataset)$out
boxplot(nh.18.sV[, c(5:8)])$out
boxplot(nh.19.sV[, c(5:8)])$out
boxplot(nh.20.sV[, c(5:8)])$out
boxplot(la.18.sV[, c(5:8)])$out
boxplot(la.19.sV[, c(5:8)])$out
boxplot(la.20.sV[, c(5:8)])$out
Figure 3. Visualization of outliers for each variable in the datasets. Top row: not.hispanic loan applicants for the years 2018, 2019 and 2020. Bottom row: latino loan applicants for the years 2018, 2019 and 2020.
Outliers can now be removed for each dataset (one variable at a time) and observations with negatives values for the income variable should also be removed for ease of understanding (Figure 4).
#eliminate outliers for each numeric variable
#NOT HISPANIC LOAN APPLICATNS - YEAR 2018
#income
outliers.nh.18.income <- boxplot(nh.18.sV[, 7])$out
describe(outliers.nh.18.income)
filtered.nh.18 <- nh.18.sV[-which(nh.18.sV[, 7] %in% outliers.nh.18.income), ]
describe(filtered.nh.18)
boxplot(filtered.nh.18[, c(5:8)])
#property value
outliers.nh.18.pv <- boxplot(filtered.nh.18[, 6])$out
describe(outliers.nh.18.pv)
filtered2.nh.18 <- filtered.nh.18[-which(filtered.nh.18[, 6] %in% outliers.nh.18.pv), ]
describe(filtered2.nh.18)
boxplot(filtered2.nh.18[, c(5:8)])
#loan amount
outliers.nh.18.la <- boxplot(filtered2.nh.18[, 5])$out
describe(outliers.nh.18.la)
filtered3.nh.18 <- filtered2.nh.18[-which(filtered2.nh.18[, 5] %in% outliers.nh.18.la), ]
describe(filtered3.nh.18)
boxplot(filtered3.nh.18[, c(5:8)])
#remove observations with negative values for income
filtered3.nh.18 <- filtered3.nh.18[filtered3.nh.18$nh18i > 0, ]
describe(filtered3.nh.18[, c(5:8)])
boxplot(filtered3.nh.18[, c(5:8)], main="Not.Hispanic loan applicants 2018")
#NOT HISPANIC LOAN APPLICATNS - YEAR 2019
#income
outliers.nh.19.income <- boxplot(nh.19.sV[, 7])$out
describe(outliers.nh.19.income)
filtered.nh.19 <- nh.19.sV[-which(nh.19.sV[, 7] %in% outliers.nh.19.income), ]
describe(filtered.nh.19)
boxplot(filtered.nh.19[, c(5:8)])
#property value
outliers.nh.19.pv <- boxplot(filtered.nh.19[, 6])$out
describe(outliers.nh.19.pv)
filtered2.nh.19 <- filtered.nh.19[-which(filtered.nh.19[, 6] %in% outliers.nh.19.pv), ]
describe(filtered2.nh.19)
boxplot(filtered2.nh.19[, c(5:8)])
#loan amount
outliers.nh.19.la <- boxplot(filtered2.nh.19[, 5])$out
describe(outliers.nh.19.la)
filtered3.nh.19 <- filtered2.nh.19[-which(filtered2.nh.19[, 5] %in% outliers.nh.19.la), ]
describe(filtered3.nh.19)
boxplot(filtered3.nh.19[, c(5:8)])
#remove observations with negative values for income
filtered3.nh.19 <- filtered3.nh.19[filtered3.nh.19$nh19i > 0, ]
describe(filtered3.nh.19[, c(5:8)])
boxplot(filtered3.nh.19[, c(5:8)], main="Not.Hispanic loan applicants 2019")
#NOT HISPANIC LOAN APPLICATNS - YEAR 2020
#income
outliers.nh.20.income <- boxplot(nh.20.sV[, 7])$out
describe(outliers.nh.20.income)
filtered.nh.20 <- nh.20.sV[-which(nh.20.sV[, 7] %in% outliers.nh.20.income), ]
describe(filtered.nh.20)
boxplot(filtered.nh.20[, c(5:8)])
#property value
outliers.nh.20.pv <- boxplot(filtered.nh.20[, 6])$out
describe(outliers.nh.20.pv)
filtered2.nh.20 <- filtered.nh.20[-which(filtered.nh.20[, 6] %in% outliers.nh.20.pv), ]
describe(filtered2.nh.20)
boxplot(filtered2.nh.20[, c(5:8)])
#loan amount
outliers.nh.20.la <- boxplot(filtered2.nh.20[, 5])$out
describe(outliers.nh.20.la)
filtered3.nh.20 <- filtered2.nh.20[-which(filtered2.nh.20[, 5] %in% outliers.nh.20.la), ]
describe(filtered3.nh.20)
boxplot(filtered3.nh.20[, c(5:8)])
#remove observations with negative values for income
filtered3.nh.20 <- filtered3.nh.20[filtered3.nh.20$nh20i > 0, ]
describe(filtered3.nh.20[, c(5:8)])
boxplot(filtered3.nh.20[, c(5:8)], main="Not.Hispanic loan applicants 2020")
#LATINO LOAN APPLICATNS - YEAR 2018
#income
outliers.la.18.income <- boxplot(la.18.sV[, 7])$out
describe(outliers.la.18.income)
filtered.la.18 <- la.18.sV[-which(la.18.sV[, 7] %in% outliers.la.18.income), ]
describe(filtered.la.18)
boxplot(filtered.la.18[, c(5:8)])
#property value
outliers.la.18.pv <- boxplot(filtered.la.18[, 6])$out
describe(outliers.la.18.pv)
filtered2.la.18 <- filtered.la.18[-which(filtered.la.18[, 6] %in% outliers.la.18.pv), ]
describe(filtered2.la.18)
boxplot(filtered2.la.18[, c(5:8)])
#loan amount
outliers.la.18.la <- boxplot(filtered2.la.18[, 5])$out
describe(outliers.la.18.la)
filtered3.la.18 <- filtered2.la.18[-which(filtered2.la.18[, 5] %in% outliers.la.18.la), ]
describe(filtered3.la.18)
boxplot(filtered3.la.18[, c(5:8)])
#remove observations with negative values for income
filtered3.la.18 <- filtered3.la.18[filtered3.la.18$la18i > 0, ]
describe(filtered3.la.18[, c(5:8)])
boxplot(filtered3.la.18[, c(5:8)], main="Latino loan applicants 2018")
#LATINO LOAN APPLICATNS - YEAR 2019
#income
outliers.la.19.income <- boxplot(la.19.sV[, 7])$out
describe(outliers.la.19.income)
filtered.la.19 <- la.19.sV[-which(la.19.sV[, 7] %in% outliers.la.19.income), ]
describe(filtered.la.19)
boxplot(filtered.la.19[, c(5:8)])
#property value
outliers.la.19.pv <- boxplot(filtered.la.19[, 6])$out
describe(outliers.la.19.pv)
filtered2.la.19 <- filtered.la.19[-which(filtered.la.19[, 6] %in% outliers.la.19.pv), ]
describe(filtered2.la.19)
boxplot(filtered2.la.19[, c(5:8)])
#loan amount
outliers.la.19.la <- boxplot(filtered2.la.19[, 5])$out
describe(outliers.la.19.la)
filtered3.la.19 <- filtered2.la.19[-which(filtered2.la.19[, 5] %in% outliers.la.19.la), ]
describe(filtered3.la.19)
boxplot(filtered3.la.19[, c(5:8)])
#remove observations with negative values for income
filtered3.la.19 <- filtered3.la.19[filtered3.la.19$la19i > 0, ]
describe(filtered3.la.19[, c(5:8)])
boxplot(filtered3.la.19[, c(5:8)], main="Latino loan applicants 2019")
#LATINO LOAN APPLICATNS - YEAR 2020
#income
outliers.la.20.income <- boxplot(la.20.sV[, 7])$out
describe(outliers.la.20.income)
filtered.la.20 <- la.20.sV[-which(la.20.sV[, 7] %in% outliers.la.20.income), ]
describe(filtered.la.20)
boxplot(filtered.la.20[, c(5:8)])
#property value
outliers.la.20.pv <- boxplot(filtered.la.20[, 6])$out
describe(outliers.la.20.pv)
filtered2.la.20 <- filtered.la.20[-which(filtered.la.20[, 6] %in% outliers.la.20.pv), ]
describe(filtered2.la.20)
boxplot(filtered2.la.20[, c(5:8)])
#loan amount
outliers.la.20.la <- boxplot(filtered2.la.20[, 5])$out
describe(outliers.la.20.la)
filtered3.la.20 <- filtered2.la.20[-which(filtered2.la.20[, 5] %in% outliers.la.20.la), ]
describe(filtered3.la.20)
boxplot(filtered3.la.20[, c(5:8)])
#remove observations with negative values for income
filtered3.la.20 <- filtered3.la.20[filtered3.la.20$la20i > 0, ]
describe(filtered3.la.20[, c(5:8)])
boxplot(filtered3.la.20[, c(5:8)], main="Latino loan applicants 2020")
#I have now the PREPARED DATASETS for running PCA
describe(filtered3.nh.18)
describe(filtered3.nh.19)
describe(filtered3.nh.20)
descibe(filtered3.la.18)
descibe(filtered3.la.19)
descibe(filtered3.la.20)
Figure 4. Boxplots visualizing the distribution of values for the numeric variables in the not.hispanic and latino loan applicants dataset for each year after the outliers observations were removed. Top row: not.hispanic loan applicants for the years 2018, 2019 and 2020. Bottom row: latino loan applicants for the years 2018, 2019 and 2020.

As we can see above, when all six libraries combined we now have a total of 712,466 loan applications for the years 2018, 2019 and 2020 from the original 1,117,251 applications that were present in the raw data. This was the result of removing applications with (a) missing values, (b) outlier values, and (c) negative values.
We can observe that the median income reported by not.hispanic loan applicants was higher for the three years compared to latino applicants; increasing by $20,000 from 2018 to 2020 for not.hispanic applicants relative to an increment of $9,000 for latinos during the same period. Interestingly, the median age for the house intended to be purchased by not.hispanic loan applicants was 10-11 years younger than houses intended to be bought by latino loan applicants that were 10-11 years older. Finally, the median loan amount requested by latinos is comparable to those requested by not.hispanic applicants even though the median property value for latinos is lower than for not.hispanics. This would mean that latinos has to borrow comparable amounts of money to not.hispanic applicants even though the properties they intend to buy are cheaper and older.
To investigate how these variables correlates among each other for latinos relative to not.hispanic loan applicants we can use the cor() function from the psych package, and we can visualize the correlation matrices created using the ggcorrplot() function from the ggcorrplot package (Figure 5).
#create correlation matrices with cor() function from the psych package
COR.filtered3.nh.18 <- cor(filtered3.nh.18[, c(5:8)], use="complete.obs")
COR.filtered3.nh.18
COR.filtered3.la.18 <- cor(filtered3.la.18[, c(5:8)], use="complete.obs")
COR.filtered3.la.18
COR.filtered3.nh.19 <- cor(filtered3.nh.19[, c(5:8)], use="complete.obs")
COR.filtered3.nh.19
COR.filtered3.la.19 <- cor(filtered3.la.19[, c(5:8)], use="complete.obs")
COR.filtered3.la.19
COR.filtered3.nh.20 <- cor(filtered3.nh.20[, c(5:8)], use="complete.obs")
COR.filtered3.nh.20
COR.filtered3.la.20 <- cor(filtered3.la.20[, c(5:8)], use="complete.obs")
COR.filtered3.la.20
#visualize correlation patterns with ggcorrplot package
install.packages("ggcorrplot", dependencies=TRUE)
library(ggcorrplot)
?ggcorrplot()
ggcorrplot(COR.filtered3.nh.18, method="circle", title="not.hispanic loan applicants - year 2018")
ggcorrplot(COR.filtered3.nh.19, method="circle", title="not.hispanic loan applicants - year 2019")
ggcorrplot(COR.filtered3.nh.20, method="circle", title="not.hispanic loan applicants - year 2020")
ggcorrplot(COR.filtered3.la.18, method="circle", title="latino loan applicants - year 2018")
ggcorrplot(COR.filtered3.la.19, method="circle", title="latino loan applicants - year 2019")
ggcorrplot(COR.filtered3.la.20, method="circle", title="latino loan applicants - year 2020")

Above are shown the correlations among variables as the output of the cor() function from the psych package.
Figure 5. Graphic output from ggcorrplot() function depicting correlations among variables for datasets from not.hispanic and latino loan applicants respectively. Top row: not.hispanic loan applicants for the years 2018, 2019 and 2020. Bottom row: latino loan applicants for the years 2018, 2019 and 2020.
In Figure 5 we can see that latino applicants differ from not.hispanic applicants in the correlation of the median_age_house variable with loan_amount and property_value variables for each dataset.
Decide how many components to extract -
A common evaluation method to decide on the number of principal components to extract is call the Catell Scree Test, in which the eigenvalues are plotted relative to their component numbers. This graph displays an elbow, indicating the components about the sharp break to be retained. A second evaluation criteria is known as the Kaiser-Harris criterion and it suggests the retention of components with eigenvalues above 1. A third evaluation run simulations that extract eigenvalues from randomly generated data matrices of the same size as the original matrix. If eigenvalues from the real data are larger than the average corresponding eigenvalues from the simulated matrices, the component is retained.
The functions available to perform this stage of PCA can be found in:
(a) screeplot() - plotting method for prcomp() and princomp() in the base implementation of R
(b) fviz_eig() - plotting method from the factoextra package
(c) fa.parallel() - plotting method from the psych package
Extract components -
Here I will use prcomp() to compute principal components and screeplot() to visualize the results. I will select and retain principal components with eigenvalues equal or greater than 1. Values in each dataset are centered and scaled (standardized).
#perform PCA using the prcomp() function
#this function uses Singular Value Decomposition (SVD) which examines the covariances / correlations between individuals
#the PCA() function from the FactoMineR package also uses SVD
?prcomp()
pca.filtered3.nh.18 <- prcomp(filtered3.nh.18[, c(5:8)], center=TRUE, scale=TRUE, rank.=2)
pca.filtered3.nh.18
summary(pca.filtered3.nh.18)
pca.filtered3.nh.19 <- prcomp(filtered3.nh.19[, c(5:8)], center=TRUE, scale=TRUE)
pca.filtered3.nh.19
summary(pca.filtered3.nh.19)
pca.filtered3.nh.20 <- prcomp(filtered3.nh.20[, c(5:8)], center=TRUE, scale=TRUE)
pca.filtered3.nh.20
summary(pca.filtered3.nh.20)
pca.filtered3.la.18 <- prcomp(filtered3.la.18[, c(5:8)], center=TRUE, scale=TRUE)
pca.filtered3.la.18
summary(pca.filtered3.la.18)
pca.filtered3.la.19 <- prcomp(filtered3.la.19[, c(5:8)], center=TRUE, scale=TRUE)
pca.filtered3.la.19
summary(pca.filtered3.la.19)
pca.filtered3.la.20 <- prcomp(filtered3.la.20[, c(5:8)], center=TRUE, scale=TRUE)
pca.filtered3.la.20
summary(pca.filtered3.la.20)

Above are shown the results from running prcomp() on each dataset. The values located on the column labeled PC1-4 are the component loadings, which are the correlations of the observed variables with the principal component. Component loadings are useful in interpreting the meaning of components. Let's now look at the proportion of variance accounted for by each component.

Above we can see that the Cumulative Proportion of Variance accounted for by the first two PCs is above 70% for all datasets. Let's now visualize the eigenvalues per component for each dataset. The eigenvalues are the standardized variance associated with a particular component.
#visualize pca results
screeplot(pca.filtered3.nh.18, type = "l", npcs = 4, main = "Screeplot of 4 PCs: not.hispanic year 2018")
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalue = 1"), col=c("red"), lty=5, cex=0.6)
screeplot(pca.filtered3.nh.19, type = "l", npcs = 4, main = "Screeplot of 4 PCs: not.hispanic year 2019")
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalue = 1"), col=c("red"), lty=5, cex=0.6)
screeplot(pca.filtered3.nh.20, type = "l", npcs = 4, main = "Screeplot of 4 PCs: not.hispanic year 2020")
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalue = 1"), col=c("red"), lty=5, cex=0.6)
screeplot(pca.filtered3.la.18, type = "l", npcs = 4, main = "Screeplot of 4 PCs: latino year 2018")
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalue = 1"), col=c("red"), lty=5, cex=0.6)
screeplot(pca.filtered3.la.19, type = "l", npcs = 4, main = "Screeplot of 4 PCs: latino year 2019")
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalue = 1"), col=c("red"), lty=5, cex=0.6)
screeplot(pca.filtered3.la.20, type = "l", npcs = 4, main = "Screeplot of 4 PCs: latino year 2020")
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalue = 1"), col=c("red"), lty=5, cex=0.6)
Figure 6. Screeplot of the eigenvalues for 4 PCs per dataset. The first 2 PCs for each dataset have eigenvalues equal to or greater than 1 and thus are retained. Top row: not.hispanic loan applicants for the years 2018, 2019 and 2020. Bottom row: latino loan applicants for the years 2018, 2019 and 2020.
Interpret Results
Using the fviz_pca_var() function from the factoextra package we can visualize the contribution of each variable to the PCs selected for each dataset, and we can compare it to plotting each loan application along the selected two PCs for a given year.
#visualize contribution of variables for the first 2 PCS in each dataset
#using the fviz_pca_var() function from factoextra package
library(factoextra)
?fviz_pca_var()
fviz_pca_var(pca.filtered3.nh.18, col.var = "contrib", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), repel = TRUE, title="not.hispanic loan applicants 2018")
fviz_pca_var(pca.filtered3.la.18, col.var = "contrib", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), repel = TRUE, title="latino loan applicants 2018")
fviz_pca_var(pca.filtered3.nh.19, col.var = "contrib", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), repel = TRUE, title="not.hispanic loan applicants 2019")
fviz_pca_var(pca.filtered3.la.19, col.var = "contrib", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), repel = TRUE, title="latino loan applicants 2019")
fviz_pca_var(pca.filtered3.nh.20, col.var = "contrib", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), repel = TRUE, title="not.hispanic loan applicants 2020")
fviz_pca_var(pca.filtered3.la.20, col.var = "contrib", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), repel = TRUE, title="latino loan applicants 2020")
#plot each loan application in 2D space
plot(pca.filtered3.nh.18$x[, 1], pca.filtered3.nh.18$x[, 2], xlab="PC1 (48%)", ylab="PC2 (25%)", main="PC1 / PC2 plot - not.hispanic loan applicant - year 2018: 170,241 applications")
plot(pca.filtered3.la.18$x[, 1], pca.filtered3.la.18$x[, 2], xlab="PC1 (47.1%)", ylab="PC2 (25.2%)", main="PC1 / PC2 plot - latino loan applicant - year 2018: 20,393 applications")
plot(pca.filtered3.nh.19$x[, 1], pca.filtered3.nh.19$x[, 2], xlab="PC1 (48%)", ylab="PC2 (25%)", main="PC1 / PC2 plot - not.hispanic loan applicant - year 2019: 192,646 applications")
plot(pca.filtered3.la.19$x[, 1], pca.filtered3.la.19$x[, 2], xlab="PC1 (47.1%)", ylab="PC2 (25.2%)", main="PC1 / PC2 plot - latino loan applicant - year 2019: 26,072 applications")
plot(pca.filtered3.nh.20$x[, 1], pca.filtered3.nh.20$x[, 2], xlab="PC1 (48%)", ylab="PC2 (25%)", main="PC1 / PC2 plot - not.hispanic loan applicant - year 2018: 272,267 applications")
plot(pca.filtered3.la.20$x[, 1], pca.filtered3.la.20$x[, 2], xlab="PC1 (47.1%)", ylab="PC2 (25.2%)", main="PC1 / PC2 plot - latino loan applicant - year 2018: 30,847 applications")
Year 2018:
Figure 7A. Visual output from the fviz_pca_var() function from the factoextra package for not.hispanic (left) and latino applicants (right) for the year 2018. Within the same PC, positive correlated variables point to the same side of the plot; whereas negative correlated variables point to opposite sides of the graph. Looking at the first PC (Dim1) for both datasets, we can see that all variables are positively correlated. However, when looking at the second PC (Dim2) it is evident that income (nh18i and la18i) is negatively correlated with median age of house (nh18mah and la18mah). The strength of the correlation is greater for latino loan applicants compared to not.hispanic loan applicants. This result supports the one shown on Figure 5.
Figure 7B. 170,241 loan applications for not.hispanic (left) and 20,393 loan applications for latino (right) were plotted in 2 dimensional space (first 2 PCs).
Year 2019:
Figure 8A. Visual output from the fviz_pca_var() function from the factoextra package for not.hispanic (left) and latino applicants (right) for the year 2019. Within the same PC, positive correlated variables point to the same side of the plot; whereas negative correlated variables point to opposite sides of the graph. Looking at the first PC (Dim1) for both datasets, we can see that all variables are positively correlated. However, when looking at the second PC (Dim2) it is evident that income (nh19i and la19i) is negatively correlated with median age of house (nh19mah and la19mah). The strength of the correlation is greater for latino loan applicants compared to not.hispanic loan applicants. This result supports the one shown on Figure 5.
Figure 8B. 192,646 loan applications for not.hispanic (left) and 26,072 loan applications for latino (right) were plotted in 2 dimensional space (first 2 PCs).
Year 2020:
Figure 9A. Visual output from the fviz_pca_var() function from the factoextra package for not.hispanic (left) and latino applicants (right) for the year 2020. Within the same PC, positive correlated variables point to the same side of the plot; whereas negative correlated variables point to opposite sides of the graph. Looking at the first PC (Dim1) for both datasets, we can see that all variables are positively correlated. However, when looking at the second PC (Dim2) it is evident that income (nh20i and la20i) is negatively correlated with median age of house (nh20mah and la20mah). The strength of the correlation is greater for latino loan applicants compared to not.hispanic loan applicants. This result supports the one shown on Figure 5.
Figure 9B. 272,267 loan applications for not.hispanic (left) and 30,847 loan applications for latino (right) were plotted in 2 dimensional space (first 2 PCs).
Interestingly, each data point in the 2D PCA plots shown above can now be colored according to any of the four categorical values we have for each dataset; mainly banks, race, sex, and action taken. Let's focus now on the variable action_taken that explains the action taken by the bank on the loan application. There are 8 possible values for this variable:
Description: The action taken on the covered loan or application
Values:
1 - Loan originated
2 - Application approved but not accepted
3 - Application denied
4 - Application withdrawn by applicant
5 - File closed for incompleteness
6 - Purchased loan
7 - Preapproval request denied
8 - Preapproval request approved but not accepted
We now from the above results that not.hispanic and latino loan applicants differ along the axis for the 2PC (Dim2) where negative correlation for income and median age of house occurs. When applying the fviz_pca_ind() function from factoextra package we can assign ellipses to colored points based on confidence intervals (95% in this case) and compare the center for each ellipse associated to a value from the action_taken variable. I am interested to see if values 3 and 7 (application denied and preapproval request denied, respectively) have different ellipses' center compared to value 6 (purchased loan) along the 2PC (Dim2). This would indicate that PCA was somehow helpful in the separation/partition of data (Figure 10).
#color data points based on action_taken by the bank
?fviz_pca_ind()
#year 2018
fviz_pca_ind(pca.filtered3.nh.18, geom.ind="point", pointshape=21, pointsize=2, fill.ind=factor(filtered3.nh.18$nh18at), col.ind=factor(filtered3.nh.18$nh18at), palette="jco", addEllipses=TRUE, ellipse.level=0.95, label="var", col.var="black", repel=TRUE, legend.title="action_taken") +
ggtitle("2D PCA-plot not.hispanic loan applicants - year 2018") +
theme(plot.title=element_text(hjust=0.5))
fviz_pca_ind(pca.filtered3.la.18, geom.ind="point", pointshape=21, pointsize=2, fill.ind=factor(filtered3.la.18$la18at), col.ind=factor(filtered3.la.18$la18at), palette="jco", addEllipses=TRUE, ellipse.level=0.95, label="var", col.var="black", repel=TRUE, legend.title="action_taken") +
ggtitle("2D PCA-plot latino loan applicants - year 2018") +
theme(plot.title=element_text(hjust=0.5))
#year 2019
fviz_pca_ind(pca.filtered3.nh.19, geom.ind="point", pointshape=21, pointsize=2, fill.ind=factor(filtered3.nh.19$nh19at), col.ind=factor(filtered3.nh.19$nh19at), palette="jco", addEllipses=TRUE, ellipse.level=0.95, label="var", col.var="black", repel=TRUE, legend.title="action_taken") +
ggtitle("2D PCA-plot not.hispanic loan applicants - year 2019") +
theme(plot.title=element_text(hjust=0.5))
fviz_pca_ind(pca.filtered3.la.19, geom.ind="point", pointshape=21, pointsize=2, fill.ind=factor(filtered3.la.19$la19at), col.ind=factor(filtered3.la.19$la19at), palette="jco", addEllipses=TRUE, ellipse.level=0.95, label="var", col.var="black", repel=TRUE, legend.title="action_taken") +
ggtitle("2D PCA-plot latino loan applicants - year 2019") +
theme(plot.title=element_text(hjust=0.5))
#year 2020
fviz_pca_ind(pca.filtered3.nh.20, geom.ind="point", pointshape=21, pointsize=10, fill.ind=factor(filtered3.nh.20$nh20at), col.ind=factor(filtered3.nh.20$nh20at), palette="jco", addEllipses=TRUE, ellipse.level=0.95, label="var", col.var="black", repel=TRUE, legend.title="action_taken") +
ggtitle("2D PCA-plot not.hispanic loan applicants - year 2020") +
theme(plot.title=element_text(hjust=0.5))
fviz_pca_ind(pca.filtered3.la.20, geom.ind="point", pointshape=21, pointsize=2, fill.ind=factor(filtered3.la.20$la20at), col.ind=factor(filtered3.la.20$la20at), palette="jco", addEllipses=TRUE, ellipse.level=0.95, label="var", col.var="black", repel=TRUE, legend.title="action_taken") +
ggtitle("2D PCA-plot latino loan applicants - year 2020") +
theme(plot.title=element_text(hjust=0.5))
Figure 10A. 2D PCA plot with data points colored according with the values from the variable action_taken by the bank on each loan application. Top row: not.hispanic loan applicants for the years 2018, 2019 and 2020. Bottom row: latino loan applicants for the years 2018, 2019 and 2020.
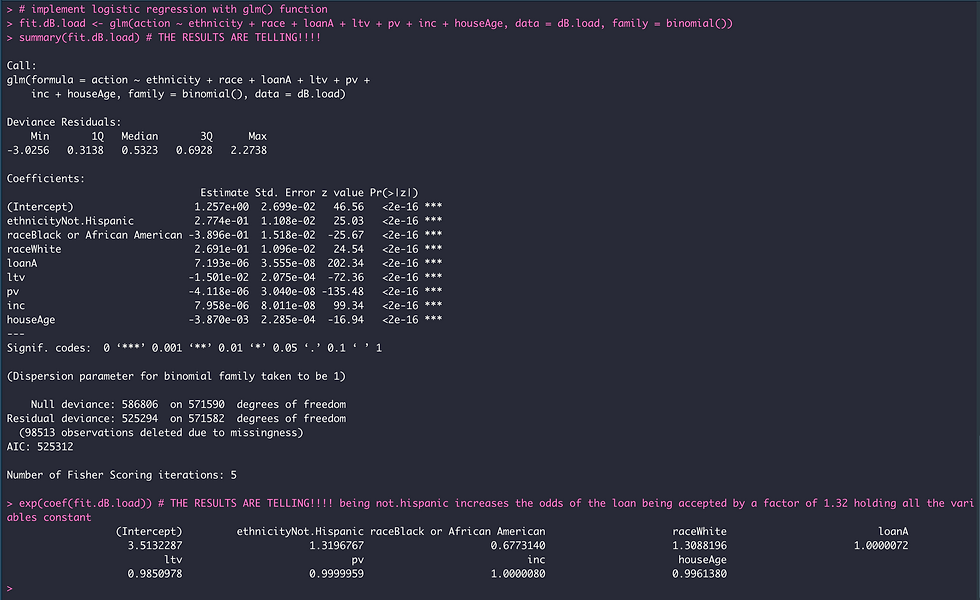
From the results shown in Figure 10, we can see that the centers for the colored ellipses for the value 6 (purchased loan) painted in red, and 7 (pre-approval request denied) painted in light blue differed most along the axis of the 2 PC (Dim2) for all datasets; whereas the center for purchased loan differed with the center for value 3 (application denied) painted in grey along the axis for PC1 (Dim1) for all datasets. This means that performing PCA was helpful to uncover an insight involving the variables in relation to the action taken by the bank on the loan application for not.hispanic and latino applicants.
References
[1] Robert L. Kabacoff (2015). R in action: data analysis and graphics with R (Second Edition). Published by Manning, Shelter Island, New York.


















































































































Comments